Resumen
El desarrollo conceptual en matemáticas es clave para que los estudiantes comprendan no solo los procedimientos, sino también los significados y relaciones entre los conceptos, lo cual promueve un aprendizaje más profundo y duradero. Esta investigación tuvo como propósito fortalecer dicha comprensión en estudiantes de sexto de secundaria mediante el diseño y aplicación de tareas centradas en la variación y el cambio, en contextos geométricos, numéricos, estocásticos y métricos. Las actividades se basaron en un subsistema de un modelo didáctico que busca articular lo conceptual con lo procedimental en el aprendizaje matemático. Se trabajó con 28 estudiantes bajo un enfoque mixto y un diseño cuasiexperimental, siguiendo tres fases: diagnóstico, diseño e implementación de tareas, y evaluación. Los resultados mostraron mejoras significativas, especialmente en los contextos numérico y estocástico, reflejadas en un aumento de estudiantes en las categorías Excelente y Bueno, y una disminución en Deficiente y Regular. En conclusión, las tareas matemáticas contextualizadas se consolidan como una estrategia eficaz para fortalecer la comprensión conceptual y su vínculo con lo procedimental. La síntesis de los resultados revela mejoras notables en los distintos contextos matemáticos, confirmando la validez y efectividad del subsistema del modelo aplicado.
Palabras clave:
Procesos variacionales; desarrollo conceptual; tareas matemáticas; educación secundaria; contextos matemáticos
Abstract
Conceptual development in mathematics is essential for students to understand not only procedures but also the meanings and relationships among concepts, which promotes deeper and more lasting learning. This research aimed to strengthen such understanding in sixth-grade secondary students through the design and implementation of tasks focused on variation and change within geometric, numerical, stochastic, and metric contexts. The activities were based on a subsystem of a didactic model that seeks to articulate conceptual understanding with procedural learning in mathematics. A total of 28 students participated under a mixed-methods and quasi-experimental design, developed in three phases: diagnosis, task design and implementation, and evaluation. The results showed significant improvements, especially in the numerical and stochastic contexts, reflected in an increase in students rated as Excellent and Good, and a decrease in those rated as Fair and Poor. In conclusion, contextualized mathematical tasks are consolidated as an effective strategy for strengthening conceptual understanding and its connection with procedural learning. The synthesis of the results reveals notable improvements across the different mathematical contexts, confirming the validity and effectiveness of the subsystem of the applied model.
Keywords:
Variational processes; conceptual development; mathematical tasks; secondary education; mathematical contexts
Introducción
La enseñanza de la matemática es esencial para el fortalecimiento de habilidades mentales, la resolución de problemas y el desarrollo del pensamiento lógico y sistemático. Sin embargo, los resultados de las pruebas PISA correspondientes a las tres últimas ediciones revelan insuficiencias en la formación matemática en la República Dominicana, con puntajes significativamente bajos en comparación con la media internacional (Organización para la Cooperación y el Desarrollo Económicos ENT#091;OECDENT#093;, 2016, 2019, 2023). Estas deficiencias apuntan a dificultades en la comprensión y aplicación de nociones matemáticas fundamentales, lo que plantea serios desafíos para el sistema educativo del país. Diversos estudios indican que uno de los principales obstáculos que enfrentan los estudiantes radica en la comprensión de los aspectos conceptuales de las matemáticas, lo que limita su desempeño en la resolución de problemas y dificulta la consolidación de aprendizajes significativos (Báez et al., 2017; Barajas et al., 2018; Naranjo & Caro, 2023).
Un factor clave en este problema es el enfoque pedagógico de muchos docentes, quienes se enfocan principalmente en la enseñanza de procedimientos y algoritmos sin profundizar en el desarrollo conceptual de la variación y el cambio. Rivadeneira & Silva (2017) sostienen que un enfoque pedagógico más eficaz debe centrarse en la edificación activa del conocimiento, promoviendo la participación de los alumnos mediante principios constructivistas, sociocríticos y de la práctica situada. Este enfoque subraya la importancia de que los estudiantes establezcan el conocimiento a través de su interacción con situaciones de la vida real, lo que facilita una comprensión más profunda de los procesos variacionales y hace el aprendizaje más significativo y duradero.
En este contexto, los procesos de variación y cambio constituyen un eje fundamental para la comprensión matemática en los contextos geométrico, numérico, estocástico y métrico (Báez, 2018). Estos aspectos son clave tanto para superar las dificultades matemáticas como para relacionar los conceptos abstractos con situaciones cotidianas, lo que favorece un aprendizaje más práctico y contextual. Sin embargo, varias investigaciones muestran que muchos docentes no abordan adecuadamente estos aspectos en sus clases, lo que dificulta que los estudiantes comprendan la relevancia y aplicabilidad de los conceptos en escenarios reales (Báez & Gómez, 2025). En este sentido, surge la pregunta de investigación: ¿Cómo impacta el diseño y la aplicación de tareas matemáticas centradas en contextos geométricos, numéricos, estocásticos y métricos, considerando los procesos variacionales, en el desarrollo conceptual de los estudiantes en secundaria?
Este estudio busca elevar la compresión de los conceptos matemáticos de los estudiantes de 6to de secundaria, utilizando como base los procesos variacionales, por medio del diseño y la aplicación de tareas matemáticas adaptativas en dichos contextos. La investigación se estructuró en tres fases: diagnóstico, intervención educativa y evaluación. Los resultados evidencian avances en la comprensión matemática por parte de los estudiantes, validando la efectividad de las tareas, las cuales fueron elaboradas atendiendo a un subsistema del modelo didáctico propuesto por Báez (2018).
Revisión de la literatura
El pensamiento variacional, según lo destacado por Mariño & Falk de Losada (2021), es un concepto clave dentro de la investigación matemática, que ha sido interpretado desde diversas perspectivas. En su tesis, presentan este tipo de razonamiento como un proceso complejo que integra aspectos variacionales, covariacionales, cuantitativos y paramétricos. Este enfoque subraya la importancia de coordinar los cambios en los valores de las variables a medida que experimentan transformaciones, lo que permite una conceptualización profunda de las cantidades como entidades que cambian de manera interrelacionada. Además, Mariño & Falk de Losada (2021), destacan que el pensamiento variacional es crucial en la construcción de una comprensión sólida de las matemáticas, ya que abarca cinco aspectos fundamentales: la variación y el cambio, la generalización, el uso de múltiples representaciones, la conexión entre aspectos dinámicos y estáticos, y la relevancia del contexto. Estos aspectos no solo facilitan la comprensión de conceptos matemáticos complejos, sino que también contribuyen al desarrollo de un pensamiento flexible y adaptativo, esencial para abordar problemas matemáticos en contextos diversos, dicho estudio sienta sus bases en Vasco (2002), quien es considerado como uno de los pioneros en el estudio de los procesos variacionales.
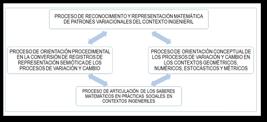
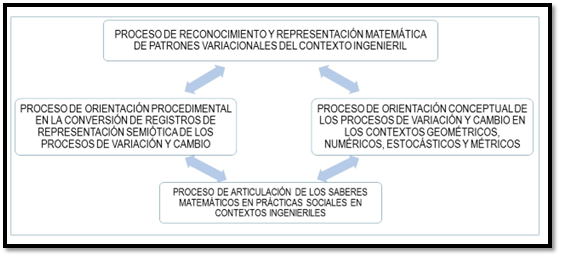
En esta misma línea, se destaca el modelo didáctico propuesto por Báez (2018) para el desarrollo conceptual procedimental en el Cálculo Diferencial de una variable real, el cual tiene como objetivo mejorar el desempeño de los estudiantes de ingeniería en la resolución de problemas matemáticos considerando los procesos variacionales como eje transversal. El mismo está estructurado por cuatro subsistemas que establecen sinergia entre sí, ilustrado en la siguiente figura 1.
Modelo didáctico de desarrollo conceptual procedimental en el PEA del CD de una variable real, para las carreras de ingeniería
La sustentación teórica del modelo atiende a tres enfoques: el Materialismo Dialéctico, considera la relación entre el conocimiento y el mundo material, enfatizando la inducción y deducción, y promoviendo la transición de lo abstracto a lo concreto. El Enfoque Histórico-Cultural, basado en las teorías de Vygotsky (1987), resalta la influencia del contexto social en el desarrollo cognitivo, subrayando la importancia de la mediación a través del lenguaje y otros signos. Por último, la Modelación Sistémica Estructural Funcional asegura que el modelo siga un enfoque sistémico, garantizando la coherencia en la relación entre los distintos subsistemas y su implementación pedagógica (Lenin, 1978; Vigotsky, 1987; Ortiz, 2011; Castilla, 2014).
Para esta investigación se asumió uno sus subsistemas del modelo para el diseño de tareas, específicamente el subsistema “Orientación conceptual de los procesos de variación y cambio en los contextos geométricos, numéricos, estocásticos y métrico”; el cual a su vez cuenta con tres componentes o pilares claves que caracterizan a las tareas elaboradas y aplicadas.
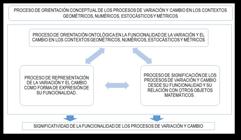
En primer lugar, el proceso de orientación ontológica en la funcionalidad tiene como función guiar al estudiante en la comprensión del significado de los objetos matemáticos a través de situaciones de variación en contextos fenomenológicos, promoviendo la predicción en escenarios geométricos, numéricos, estocásticos y métricos. Luego, el proceso de representación de la variación como forma de expresión de su funcionalidad permite al estudiante analizar la representación matemática del cambio y la variación mediante la modelación y graficación, enfatizando que las argumentaciones matemáticas están estructuradas por significados, procedimientos y procesos. Finalmente, el proceso de significación de los procesos de variación desde su funcionalidad y su relación con otros objetos matemáticos orienta al estudiante en la interpretación de la modelación matemática de situaciones variacionales en diferentes contextos, facilitando la articulación de los significados de procedimientos, objetos y procesos matemáticos.
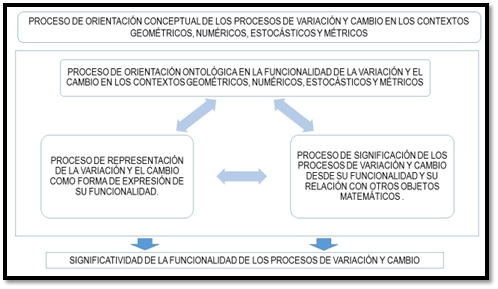
Estos tres componentes están interconectados de manera coordinada, tal y como se muestra en la figura 2, permitiendo así la caracterización de los rasgos esenciales de los objetos matemáticos en distintos contextos. Esta organización favorece la construcción de significatividad en la funcionalidad de los procesos matemáticos, lo que permite al estudiante interpretar el carácter funcional de los conceptos matemáticos y comprender la relación entre procedimientos, procesos-objetos y argumentaciones dentro del aprendizaje matemático.
Subsistema: orientación conceptual de los procesos de variación y cambio en los contextos geométricos, numéricos, estocásticos y métricos
A continuación, presentamos el caso particular de la tarea “El Movimiento de un Columpio como Modelo de Oscilación”. Esto con el fin de que se pueda apreciar, cómo se pueden diseñar tareas que promuevan el desarrollo conceptual atendiendo a los procesos de variación y cambio según el subsistema del modelo planteado.
El movimiento de un columpio es un caso ideal para introducir el estudio de las funciones periódicas y su relación con la velocidad y la aceleración. En esta tarea, los estudiantes modelarán matemáticamente su movimiento mediante gráficas y ecuaciones, explorando la variación y el cambio en distintos contextos.
Desde el Proceso de Orientación Ontológica en la Funcionalidad de la Variación y el Cambio, se busca que los estudiantes identifiquen cómo estos conceptos se manifiestan en el movimiento oscilatorio del columpio. Para ello, la actividad comienza con la observación directa de un columpio en un parque o, en su defecto, a través de un video o simulación digital. Posteriormente, el docente plantea preguntas que fomentan la reflexión y el análisis cualitativo del fenómeno: ¿Cómo cambia la posición del columpio a lo largo del tiempo? ¿En qué momentos se mueve más rápido y en cuáles se detiene? ¿Cómo variaría su movimiento en ausencia de fricción y resistencia del aire? Estas preguntas permiten que los estudiantes comiencen a identificar regularidades en el movimiento y establezcan relaciones entre la posición y el tiempo.
Los estudiantes suelen notar que el columpio oscila de un extremo a otro con un movimiento repetitivo. También reconocen que la velocidad es máxima en el punto central y se anula en los extremos antes de invertir la dirección. Ante la pregunta sobre la fricción, algunos mencionan que, en un sistema ideal sin resistencia, el columpio continuaría oscilando indefinidamente sin perder amplitud, lo que introduce la idea de un sistema oscilatorio ideal.
Como parte del Proceso de Representación de la Variación y el Cambio como Forma de Expresión de su Funcionalidad, una vez comprendido el comportamiento cualitativo del columpio, el docente introduce la necesidad de modelarlo matemáticamente. Para guiar este proceso, plantea preguntas clave como: ¿Cómo podríamos representar matemáticamente la posición del columpio en cualquier instante de tiempo? ¿Por qué la gráfica de su movimiento no es una línea recta y qué nos indica su forma? ¿Qué características de la oscilación debemos considerar al construir el modelo? Estas interrogantes fomentan la reflexión sobre la naturaleza del movimiento oscilatorio y orientan a los estudiantes en la formulación de un modelo preciso.
Los estudiantes pueden sugerir la representación del movimiento mediante un diagrama o el registro de posiciones en una tabla de datos. A partir de esto, reconocen que la gráfica obtenida no es lineal, sino que tiene una forma ondulatoria. Algunos identifican que este tipo de movimiento se asemeja a la gráfica de funciones trigonométricas. Para modelar matemáticamente el movimiento oscilatorio del columpio, se asume que su posición en función del tiempo puede describirse mediante una función seno o coseno (Swokowski & Cole, 2022). Si tomamos como referencia el punto de equilibrio, la ecuación que describe su movimiento es:
Donde:
Si el columpio parte desde su máxima posición a la derecha ( 𝐴 ), la ecuación se simplifica a:
Para un columpio con 𝐴=1.5 metros y un período 𝑇=4 segundos:
Por lo tanto, la ecuación del movimiento es:
En el Proceso de Significación de los Procesos de Variación y Cambio desde su Funcionalidad y su Relación con otros Objetos Matemáticos, se busca que los estudiantes interpreten el modelo matemático y comprendan su vínculo con otros conceptos. Para ello, el docente plantea preguntas como: Si conocemos la posición en función del tiempo, ¿cómo podríamos determinar la velocidad del columpio? ¿En qué momentos la velocidad es máxima y cuándo es cero? ¿Qué implica el cambio de velocidad en términos de aceleración?
Los estudiantes pueden intuir que la velocidad es máxima en el punto central y nula en los extremos. Para confirmar esto, se calcula la velocidad derivando la ecuación de la posición:
Esto indica que la velocidad sigue una función seno, alcanzando su valor máximo en el punto central. Para obtener la aceleración, derivamos nuevamente:
Esto muestra que la aceleración es proporcional a la posición, pero en sentido contrario, lo que es característico del movimiento oscilatorio.
Finalmente, el docente cierra la actividad con preguntas como: ¿Qué nos indica la relación entre posición, velocidad y aceleración? ¿Cómo podríamos representar estos tres aspectos en una misma gráfica? ¿Por qué este modelo es útil para analizar otros fenómenos físicos? Estas preguntas permiten que los estudiantes comprendan que el movimiento oscilatorio es un concepto fundamental en diversas disciplinas, desde la mecánica hasta la electrónica.
Métodos
Este estudio se llevó a cabo bajo un enfoque metodológico cuantitativo, con un diseño cuasi-experimental y un alcance descriptivo. Se trata de un artículo original, cuyo propósito fue caracterizar el desempeño de los estudiantes antes y después de una intervención educativa, y analizar cómo esta intervención impactó en su aprendizaje (Hernández Sampieri et al., 2014).
El objetivo general de la investigación fue fortalecer el desarrollo conceptual de los estudiantes de sexto de secundaria mediante la implementación de tareas matemáticas contextualizadas en distintos dominios -geométrico, numérico, estocástico y métrico-, centradas en los procesos de variación y cambio. Los objetivos específicos fueron:
-
Diagnosticar el nivel de comprensión conceptual de los estudiantes en los distintos contextos matemáticos antes de la intervención.
-
Diseñar e implementar tareas que integren la variación y el cambio en contextos múltiples.
-
Evaluar el impacto de la intervención en el desempeño conceptual posterior de los estudiantes.
La metodología se desarrolló en tres fases. La primera fue una etapa diagnóstica inicial, orientada a detectar fortalezas y debilidades en el desarrollo conceptual de los estudiantes, centrado en patrones de variación dentro de contextos geométricos, numéricos, estocásticos y métricos. La segunda fase consistió en la intervención educativa, que incluyó tareas matemáticas diseñadas específicamente para promover la identificación, análisis y aplicación de dichos patrones. Finalmente, en la tercera fase, se realizó una evaluación para medir el impacto de la intervención en el desarrollo conceptual de los participantes. Para establecer una línea base, se aplicó inicialmente un cuestionario diagnóstico que permitió evaluar los conocimientos previos.
La propuesta didáctica estuvo basada en el subsistema “Orientación conceptual de los procesos de variación y cambio”, parte del modelo didáctico de desarrollo conceptual y procedimental en cálculo diferencial. Este subsistema gira en torno a tres ejes: la orientación ontológica del concepto de variación y cambio, su representación a través de distintas formas funcionales, y su interpretación en relación con otros objetos matemáticos.
La población del estudio estuvo compuesta por 28 estudiantes de sexto grado de secundaria, seleccionados mediante muestreo no probabilístico por conveniencia. Durante el ciclo académico se recopilaron datos a través de formularios estructurados. El formulario de entrada constó de 16 preguntas, agrupadas en cuatro secciones temáticas: ecuaciones lineales, ecuaciones cuadráticas, inecuaciones, y sucesiones y progresiones (cuatro preguntas por sección). El cuestionario de salida, por su parte, incluyó 20 ítems: cinco sobre Trigonometría, cinco sobre Límite, cinco sobre Derivada y cinco relacionados con Integrales Básicas. Dado que participaron estudiantes menores de edad, se contó con la autorización del centro educativo y el consentimiento informado de padres o tutores.
Ambos instrumentos fueron validados por tres expertos en matemática y didáctica, quienes evaluaron la pertinencia, claridad y coherencia de los ítems. La confiabilidad se determinó mediante el coeficiente Alfa de Cronbach, obteniéndose un valor de 0.87, indicador de una adecuada consistencia interna. Para el análisis de los datos se empleó exclusivamente estadística descriptiva, lo cual constituye una limitación del estudio al no incorporar análisis inferenciales.
Con el propósito de interpretar los resultados obtenidos en ambas evaluaciones, se estableció una escala de calificación basada en el porcentaje de aciertos. Esta escala permitió clasificar el desempeño de los estudiantes en cuatro niveles: excelente, bueno, regular y deficiente, ajustándose proporcionalmente al número total de ítems en cada cuestionario.
Resultados
En lo adelante, se presentarán las derivaciones del estudio, centrados en el análisis de los avances conceptuales alcanzados por los estudiantes en los contextos tratados durante la intervención.
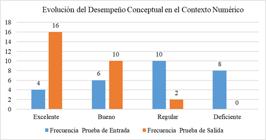
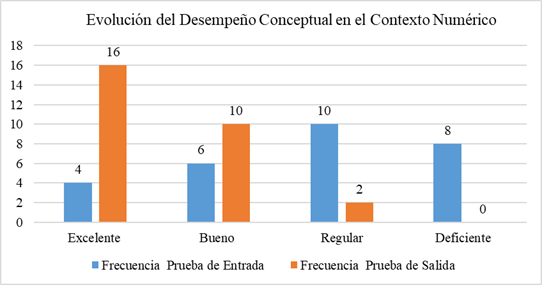
La comparación entre las pruebas de entrada y salida muestra una mejora significativa en el desempeño conceptual de los estudiantes en el contexto numérico. Inicialmente, el 64.3% de los estudiantes estaba en las categorías Regular y Deficiente. Tras la intervención, el 57.1% alcanzó un nivel Excelente y el 35.7% un desempeño Bueno, reduciendo a solo el 7.1% los niveles bajos. Esto evidencia que la intervención fue eficaz para mejorar la comprensión y desempeño en los procesos de variación y cambio numéricos.
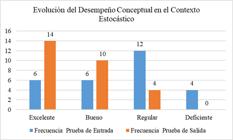
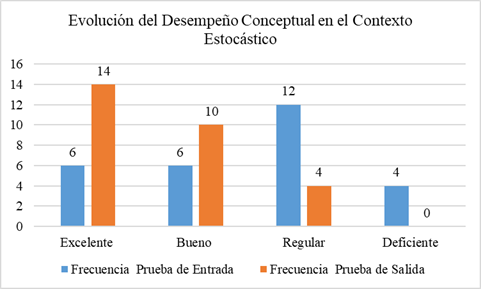
El análisis del desempeño conceptual en el contexto estocástico muestra un progreso significativo tras la intervención. Inicialmente, el 60.7% de los estudiantes estaba en las categorías Regular y Deficiente. En la prueba de salida, el 50% alcanzó la categoría Excelente y el 35.7% mostró un desempeño Bueno. Esto redujo los niveles bajos al 14.3%, evidenciando una mejora notable en la comprensión y desempeño gracias a la intervención.
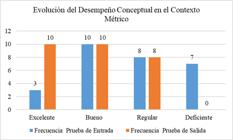
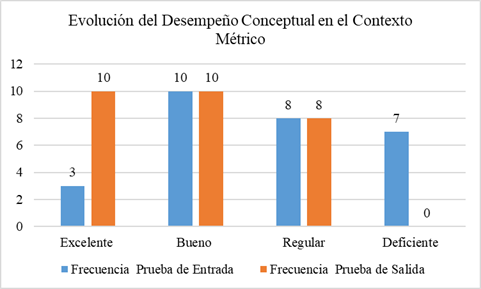
El análisis del desempeño conceptual en el contexto métrico revela una mejora notable tras la intervención. En la prueba de entrada, solo el 10.7% de los estudiantes alcanzó la categoría Excelente y el 25% estaba en Deficiente. En la prueba de salida, el nivel Excelente aumentó al 35.7%, y ningún estudiante quedó en la categoría Deficiente. Estos resultados evidencian un progreso significativo en la comprensión de los conceptos métricos.
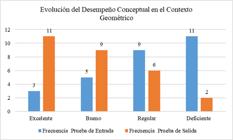
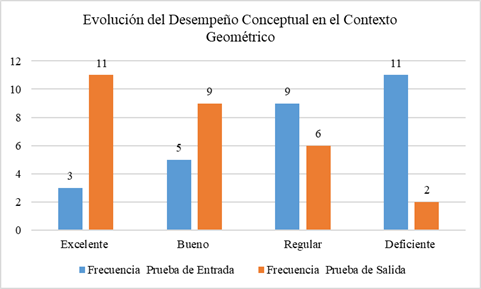
El análisis del desempeño en el contexto geométrico muestra una mejora significativa tras la intervención. En la prueba de entrada, solo el 10.7% alcanzó la categoría Excelente, mientras que un 39.3% estuvo en Deficiente. En la prueba de salida, el 39.3% alcanzó Excelente, y la categoría Deficiente se redujo al 7.1%. Esto refleja un notable progreso en la comprensión de los conceptos geométricos, evidenciando el impacto positivo de la intervención.
En general, los resultados obtenidos en las cuatro categorías de desempeño conceptual (numérico, estocástico, métrico y geométrico) reflejan una mejora significativa en los estudiantes tras la intervención. En la prueba de entrada, la generalidad de los estudiantes se ubicaba en los niveles de Regular y Deficiente, con un bajo porcentaje en los niveles Excelente y Bueno en todos los contextos evaluados. Sin embargo, en la prueba de salida, se observó un aumento valioso en el número de alumnos que alcanzaron los niveles Excelente y Bueno, mientras que las categorías Deficiente y Regular disminuyeron considerablemente. Este cambio positivo es especialmente evidente en los contextos numérico y estocástico, donde la mejora fue más pronunciada. Los resultados sugieren que la intervención tuvo un impacto positivo en el desarrollo conceptual de los estudiantes, favoreciendo una mayor comprensión de los conceptos clave en los distintos contextos matemáticos evaluados.
4.1. Discusión de los resultados
Los resultados obtenidos en esta investigación muestran un avance sustancial en la comprensión conceptual de los estudiantes de secundaria, confirmando la efectividad de las tareas diseñadas desde la perspectiva del pensamiento variacional. El incremento en los niveles de desempeño Excelente y Bueno, especialmente en los contextos numérico y estocástico, evidencia que las actividades propuestas lograron provocar un cambio positivo en la forma en que los estudiantes se aproximan al conocimiento matemático.
Este hallazgo guarda estrecha relación con lo planteado por Báez (2018), quien sostiene que la orientación conceptual de los procesos de variación y cambio favorece la articulación entre el significado, la representación y la argumentación en la enseñanza de la matemática. De igual modo, coincide con Mariño & Falk de Losada (2021), quienes señalan que el pensamiento variacional no solo permite comprender el cambio y la covariación entre magnitudes, sino que desarrolla una visión más flexible y profunda de las relaciones matemáticas.
En comparación con estudios previos, los resultados de esta investigación amplían los planteamientos de Barajas, Parada & Molina (2018), quienes reportaron dificultades persistentes en el razonamiento variacional al resolver problemas contextualizados. En el presente estudio, el uso de tareas ancladas en situaciones reales -como el movimiento de un columpio, inspirado en el trabajo de Swokowski & Cole (2022)- permitió que los estudiantes establecieran vínculos más sólidos entre la representación algebraica, gráfica y funcional.
De igual modo, el progreso observado responde a las recomendaciones de Rivadeneira & Silva (2017), al incorporar principios de aprendizaje activo y mediación docente bajo un enfoque constructivista y sociocrítico. La interacción entre el estudiante y el contexto, así como la reflexión sobre sus propias estrategias, propiciaron una reconstrucción significativa del conocimiento. Este proceso se vio reforzado por la dimensión social del aprendizaje descrita por Vigotsky (1987), donde la colaboración y la mediación del lenguaje favorecieron la apropiación de los conceptos matemáticos.
Por otro lado, los casos en que algunos estudiantes permanecieron en niveles Regular o Deficiente reflejan la persistencia de brechas asociadas a la rigidez del pensamiento procedimental. Esto coincide con lo expresado por Star (2005), quien advierte que el dominio de algoritmos no garantiza la comprensión conceptual si no se acompaña de una reflexión sobre el porqué de los procedimientos. En este sentido, se hace necesario fortalecer la intervención con estrategias más personalizadas y andamiajes diferenciados, que tomen en cuenta la diversidad cognitiva y los distintos ritmos de aprendizaje.
En síntesis, los hallazgos confirman que las tareas basadas en la variación y el cambio no solo desarrollan habilidades matemáticas, sino que transforman la manera en que los estudiantes piensan y se relacionan con las matemáticas. Esta transformación se traduce en avances conceptuales evidentes, que concuerdan con las bases teóricas de Ortiz (2011) y Lenin (1978) sobre la necesidad de entender el conocimiento como un proceso dialéctico, donde lo concreto y lo abstracto se entrelazan de manera dinámica.
Conclusiones
Los resultados de esta investigación permiten concluir que la implementación de tareas matemáticas contextualizadas en distintos contextos geométrico, numérico, estocástico y métrico, sustentadas en el subsistema “Orientación conceptual de los procesos de variación y cambio” del modelo didáctico de Báez (2018), favorece de manera significativa el desarrollo conceptual de los estudiantes de secundaria, lo cual se corresponde con el objetivo general de esta investigación.
El avance observado en los niveles Excelente y Bueno demuestra que las tareas diseñadas desde el pensamiento variacional promovieron la articulación entre el significado, la representación y la argumentación matemática, validando la afirmación de Báez (2018) de que este enfoque “fortalece la conexión entre lo conceptual y lo procedimental en la enseñanza de la matemática”.
Asimismo, los resultados confirman que la comprensión del cambio en diversos contextos, como señala Mariño & Falk de Losada (2021), desarrolla una visión más flexible y profunda de las relaciones matemáticas.
Este principio se materializó al vincular los procesos variacionales con fenómenos reales, generando aprendizajes más significativos.
Finalmente, se reconoce que el subsistema aplicado del modelo didáctico constituye una herramienta efectiva para orientar la enseñanza de las matemáticas hacia una comprensión más profunda, contextual y funcional, reafirmando la pertinencia de integrar los procesos de variación y cambio como eje transversal en la educación secundaria.
Agradecimientos y reconocimientos
Se expresa el agradecimiento al Ministerio de Educación Superior, Ciencia y Tecnología (MESCyT) de la República Dominicana, por su apoyo a través del Fondo Nacional de Innovación y Desarrollo Científico y Tecnológico (FONDOCYT), quien financió el proyecto FONDOCYT 2020-2021-2B4-182 titulado “Estrategia Didáctica para el Desarrollo Conceptual Procedimental en los Procesos de Enseñanza-Aprendizaje del Cálculo Diferencial y su Efecto en el Desempeño Autónomo de Estudiantes Dominicanos en la Solución de Problemas Matemáticos”.
Asimismo, se reconoce el respaldo de la Universidad ISA, como el órgano gestor del proyecto, por proporcionar el apoyo institucional necesario para su desarrollo y ejecución.
Referencias bibliográficas
- Báez, A. M. (2018). Estrategia didáctica para el desarrollo conceptual procedimental en el cálculo diferencial de una variable real, para las carreras de ingeniería ENT#091;Tesis doctoral, Universidad de Camagüey “Ignacio Agramonte Loynaz”, Centro de Estudios de Ciencias de la Educación “Enrique José Varona”ENT#093;.
-
Báez, A. M., & Gómez Muñoz, H. (2025). Dificultades en el diseño de tareas matemáticas de desarrollo procedimental de procesos de variación y cambio: Un estudio con docentes dominicanos. Transformación, 21(e-486). https://transformation.reduc.edu.cu/index.php/transformacion/article/view/486/561
» https://transformation.reduc.edu.cu/index.php/transformacion/article/view/486/561 -
Báez, A. M., Pérez-González, O. L., & Triana-Hernández, B. (2017). Propuesta didáctica basada en múltiples formas de representación semiótica de los objetos matemáticos para desarrollar el proceso de enseñanza-aprendizaje del cálculo diferencial. Academia y Virtualidad, 10(2), 20-30. https://doi.org/10.18359/ravi.2743
» https://doi.org/10.18359/ravi.2743 -
Barajas, C., Parada, S., & Molina, J. (2018). Análisis de dificultades surgidas al resolver problemas de variación. Educación Matemática, 30(3), 297-323. https://doi.org/10.24844/em3003.12
» https://doi.org/10.24844/em3003.12 -
Castilla, M. (2014). La teoría del desarrollo cognitivo de Piaget aplicada en la clase de Primaria ENT#091;Trabajo de fin de grado, Universidad de ValladolidENT#093;. https://uvadoc.uva.es/handle/10324/5844
» https://uvadoc.uva.es/handle/10324/5844 - Hernández Sampieri, R., Fernández Collado, C., & Baptista Lucio, P. (2014). Metodología de la investigación (6.ª ed.). McGraw-Hill Education.
- Lenin, V. I. (1978). Las tres fuentes y las tres partes integrantes del marxismo. Editorial de Ciencias Sociales. (Trabajo original publicado en 1913).
-
Mariño, L. F., & Falk de Losada, M. (2021). Avances en la caracterización del pensamiento variacional emergente en el contexto del planteo y resolución de problemas en profesores de matemáticas en formación. Universidad Antonio Nariño. https://cienciaabierta.uan.edu.co/Record/repositorio.uan.edu.co-123456789-2241/Description?sid=191034
» https://cienciaabierta.uan.edu.co/Record/repositorio.uan.edu.co-123456789-2241/Description?sid=191034 -
Naranjo, D., & Caro, J. (2023). Fortalecimiento de problemas de aplicación del pensamiento variacional a través de la metodología del juego como estrategia pedagógica ENT#091;Tesis de pregrado, Universidad Cooperativa de ColombiaENT#093;. Repositorio Institucional UCC. https://repository.ucc.edu.co/entities/publication/5604c56d-b621-4731-bb77-615d297f8ff6
» https://repository.ucc.edu.co/entities/publication/5604c56d-b621-4731-bb77-615d297f8ff6 -
Organización para la Cooperación y el Desarrollo Económicos (OECD). (2016). PISA 2015 results (Volume I): The state of learning and equity in education. OECD Publishing. https://www.oecd.org/fr/publications/resultats-du-pisa-2015-volume-i_9789264267534-fr.html
» https://www.oecd.org/fr/publications/resultats-du-pisa-2015-volume-i_9789264267534-fr.html -
Organización para la Cooperación y el Desarrollo Económicos (OECD). (2019). PISA 2018 results (Volume I): The state of learning and equity in education. OECD Publishing. https://www.oecd.org/fr/publications/resultats-du-pisa-2018-volume-i_ec30bc50-fr.html
» https://www.oecd.org/fr/publications/resultats-du-pisa-2018-volume-i_ec30bc50-fr.html -
Organización para la Cooperación y el Desarrollo Económicos (OECD). (2023). PISA 2022 results (Volume I): The state of learning and equity in education. OECD Publishing. https://www.oecd.org/en/publications/pisa-2022-results-volume-i_53f23881-en.html
» https://www.oecd.org/en/publications/pisa-2022-results-volume-i_53f23881-en.html -
Ortiz, E. (2011). La dialéctica en las investigaciones educativas. Revista Electrónica Actualidades Investigativas en Educación, 11(2), 1-26. https://www.redalyc.org/pdf/447/44720020023.pdf
» https://www.redalyc.org/pdf/447/44720020023.pdf -
Rivadeneira, E., & Silva, R. (2017). Aprendizaje basado en la investigación en el trabajo autónomo y en equipo. Negotium, 13(38), 5-16. https://www.redalyc.org/pdf/782/78253678001.pdf
» https://www.redalyc.org/pdf/782/78253678001.pdf -
Star, J. (2005). Reconceptualizing procedural knowledge. Journal for Research in Mathematics Education, 36(5), 404-411. https://pcl.sitehost.iu.edu/rgoldsto/courses/cogscilearning/starprocedural.pdf
» https://pcl.sitehost.iu.edu/rgoldsto/courses/cogscilearning/starprocedural.pdf -
Swokowski, E. W., & Cole, J. A. (2022). Álgebra y trigonometría con geometría analítica (12.ª ed.). Edamsa Impresiones, S.A. de C.V. https://profedion.wordpress.com/wp-content/uploads/2019/06/algebra-y-trigonometria-con-geometria-analitica-12ed.pdf
» https://profedion.wordpress.com/wp-content/uploads/2019/06/algebra-y-trigonometria-con-geometria-analitica-12ed.pdf -
Vasco, C. E. (2002). El pensamiento variacional, la modelación y las nuevas tecnologías. En Congreso Internacional Tecnologías Computacionales en el Currículo de Matemáticas: Actas electrónicas del Congreso (Blumenau, Brasil). https://funes.uniandes.edu.co/wp-content/uploads/tainacan-items/32454/1142293/Vasco2002El.pdf
» https://funes.uniandes.edu.co/wp-content/uploads/tainacan-items/32454/1142293/Vasco2002El.pdf - Vigotsky, L. S. (1987). Historia del desarrollo de las funciones psíquicas superiores. Editorial Científico-Técnica.
Fechas de Publicación
-
Publicación en esta colección
10 Set 2025 -
Fecha del número
Jul-Dec 2025
Histórico
-
Recibido
15 Feb 2025 -
Acepto
10 Set 2025

 Tareas matemáticas en contextos múltiples para fortalecer el desarrollo conceptual mediante patrones variacionales en secundaria
Tareas matemáticas en contextos múltiples para fortalecer el desarrollo conceptual mediante patrones variacionales en secundaria