Abstract
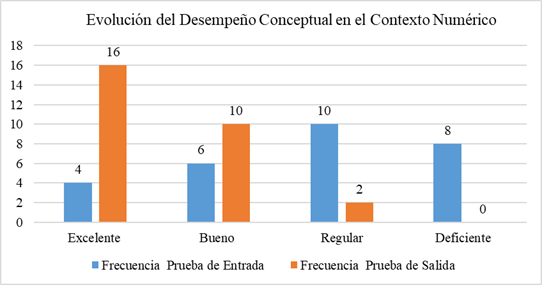
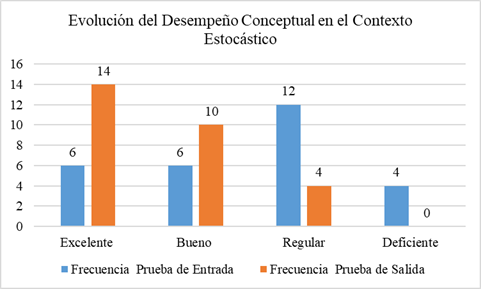
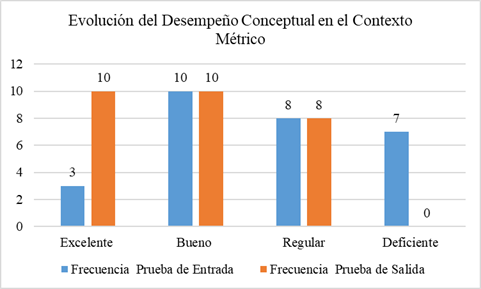
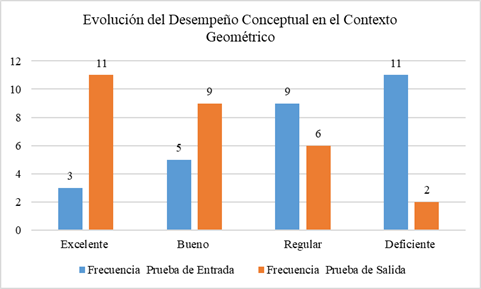
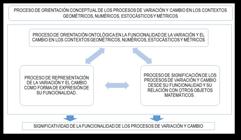
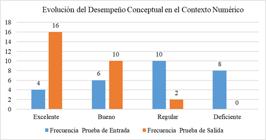
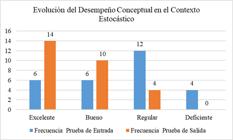
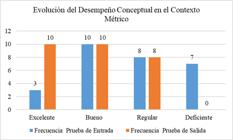
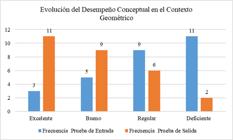
Conceptual development in mathematics is essential for students to understand not only procedures but also the meanings and relationships among concepts, which promotes deeper and more lasting learning. This research aimed to strengthen such understanding in sixth-grade secondary students through the design and implementation of tasks focused on variation and change within geometric, numerical, stochastic, and metric contexts. The activities were based on a subsystem of a didactic model that seeks to articulate conceptual understanding with procedural learning in mathematics. A total of 28 students participated under a mixed-methods and quasi-experimental design, developed in three phases: diagnosis, task design and implementation, and evaluation. The results showed significant improvements, especially in the numerical and stochastic contexts, reflected in an increase in students rated as Excellent and Good, and a decrease in those rated as Fair and Poor. In conclusion, contextualized mathematical tasks are consolidated as an effective strategy for strengthening conceptual understanding and its connection with procedural learning. The synthesis of the results reveals notable improvements across the different mathematical contexts, confirming the validity and effectiveness of the subsystem of the applied model.
Keywords:
Variational processes; conceptual development; mathematical tasks; secondary education; mathematical contexts

 Mathematical tasks in multiple contexts to strengthen conceptual development through variational patterns in secondary education
Mathematical tasks in multiple contexts to strengthen conceptual development through variational patterns in secondary education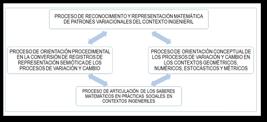 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail